스트럿타이모델 Strut Tie model(STM)

1.0 스트럿타이모델 Strut Tie model(STM) 소개

1.1스트럿타이모델 Strut Tie model(STM) 이란

콘크리트 구조 부재의 설계를 위해 트러스 모델을 콘크리트 압축력을 나타내는 스트럿, 철근에 작용하는 인장력을 나타내는 타이, 그리고 스트럿과 타이가 만나는 절점영역 등으로 이상화 시킨 것으로서, 복잡한 하중조건 및 기하학적 형상으로 인해 응력흐름이 복잡한 콘크리트 구조부재의 합리적인 설계를 가능하게 한다. (참고)

뿐만 아니라 스트럿-타이 모델 방법은 균열 발생 전은 물론이고, 균열 발생 후에도 구조부재 내부의 하중의 재분배를 예측할 수 있다. (참고)

응력장 이론(Stress Field Theory)과Strut-Tie Model 이 있다. 응력장 이론이 이론적으로는 우수하다고 할 수 있으나, 실무에서는 보다 직관적인 Strut-Tie Model이 널리 쓰인다.

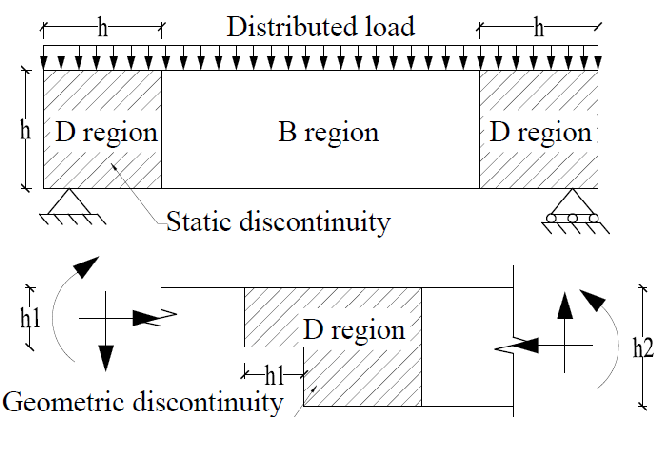
일반적으로 전단지간이 큰 형태로 하중을 지지하여 단면 변형률이 선형으로 되어 있는 구간(B영역) 은 일반적인 보이론을 적용하여 검토하지만, 전단 지간이 작아 아치작용에 의하여 하중이 지지되는 응력교란이 심한 그리고 보 이론을 적용할 수 없는구간(D영역)에 Strut-Tie Model을 이용하여 설계한다. (2.0 B영역과 D영역 참고)

1.2 스트럿타이모델 Strut Tie model(STM) 의 어려움

그러나 스트럿-타이 모델 방법에 의한 콘크리트 구조부재의 해석 및 설계과정은 스트럿 및 절점영역의 강도조건을 만족시키는 스트럿-타이 모델의 형성, 스트럿 및 절점영역의 유효강도 결정, 스트럿 및 타이의 필요단면적과 단면력의 결정, 스트럿 및 절점영역 경계면의 최대단면적 결정, 그리고 스트럿 및 절점영역의 강도조건의 검토 등으로 인한 여러 반복적인 수치해석과정, 많은 도식적 계산과정, 그리고 여러 단계에서의 설계자의 주관적인 판단 등을 필요로 하는 단점이 있다. 

1.3 스트럿타이모델 기준

콘크리트구조 설계(강도설계법) 일반사항 KDS 14 20 01 :2022

콘크리트구조 스트럿-타이모델 기준 KDS 14 20 24 :2021

2.0 B영역과 D영역

2.1 B영역

보이론 평면유지 베르누이법칙 의 가정이 성립함. Beam또는 베르누이(Bernoulli)의 첫글자를 따 B영역이다. 보의 전단경간이 커서 보 작용에 의하여 하중이 지지되며, 단면 변형률이 선형으로 되어 평면보존의 법칙이 성립되는 부분을 말한다.

NOTE:일러-베르누이(Euler-Bernoulli) 보 이론에 근거한 보이다. 오일러-베르누이 보는 두 개의 보가 연결되어 있는 경우, 변형이 발생하면 연속으로 이동 변위와 회전 변위를 가져야 한다. 다시 말하면, 보의 연결 절점에서 ‘이동’ 변위와 ‘회전’ 변위는 동일하다. 따라서 이 이론은 변형 이전의 중립축에 수직인 평면은 변형이 일어난 후에도 중립축에 수직으로 남는다는 가정에 바탕을 둔 이론이다. 이 보는 Thin Beam 이라고도 한다.

2.2 D영역

보이론 평면유지 베르누이법칙 의 가정이 성립하지 않는다. 응력교란(Disturbed) 또는 단면의 불연속(Discontinuity)의 머리 글자를 따 D 영역이다. 전단경간이 작아서 아치작용에 의하여 하중이 지지되며, 보 이론을 적용할 수 없는 부분을 말한다.

일반적인 구조부재에서는 집중하중 및 지반반력이 작용하는 영역, 브래킷 또는 내민받침, 보-기둥의 연결부, 턱이진 보의 단부, 단면이나 단면력이 급변하는 곳, 개구부가 있는 부재, 프리텐션 및 포스트텐션 콘크리트 구조부재의 정착부, 그밖에 기하학적 불연속부 등

(Tjhin and Kuchma, 2002)

(STRUT-AND-TIE MODELS FOR DEFORMATION OF REINFORCED CONCRETE BEAM-COLUMN JOINTS DEPENDENT ON PLASTIC HINGE BEHAVIOR OF BEAMS)

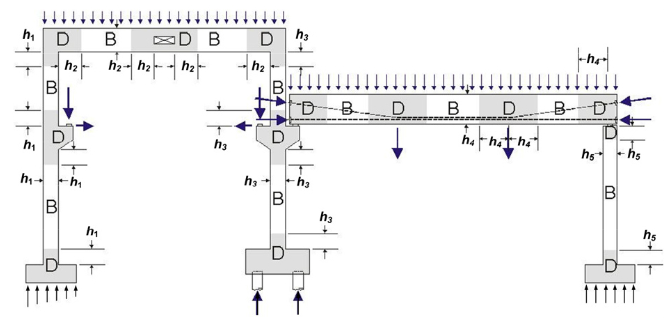
2.3 B영역과 D영역의 구분

원리 자체가 정확한 것은 아지만 생브낭의 원리 적용하여 1/h 법으로 아래와 같이 B영역과 D영역을 구분한다.

3.0 STM 구성요소

• 압축재 (스트럿)
• 인장재 (타이)
• 절점구역

3.1 압축재

 Φc 스트럿의 강도감소계수로 0.75

β 는 각 조건에 따라 다음과 같이 구하여야 한다.

1. 전 길이에 걸쳐 스트럿의 단면적이 일정할 경우 1.0
2. 스트럿 길이 중앙부의 단면적이 스트럿 양단의 단면적보다 큰 병모양인 스트럿의 경우 4.2.3의 철근 배치에 관한 규정을 만족할 때=0.75이며, 그렇지 못할 때 =0.60 이다. 여기서, λ는 KDS 14 20 10(4.4)에 따른다.
3. 인장요소 또는 콘크리트 구조 부재의 인장플랜지 콘크리트의 스트럿인 경우 0.40
4. 기타의 모든 경우 0.60

Wprov는 아래로 산정

3.2 인장재

Φs 타이의 강도감소계수로 0.85

3.3 절점구역

• CCC절점
• CCT절점
• CTT절점
• TTT절점

다른 컨텐츠

Section Properties Calculator Including Allowable Stress (1)